Volume (Triple) Integrals – Josh The Engineer

In this article I’ll be going through what I think is an intuitive explanation of a volume (or triple) integral in relation to the conservation equations. I’m laying out the volume integral before I go through the less-intuitive surface integral in my next post. As a quick note, I usually write the volume as a $V$ with a strike-through, but I can’t do this using the WordPress Latex interpreter, so whenever you see a normal capital $V$ , don’t confuse it with the velocity vector, $\vec{V}$ .

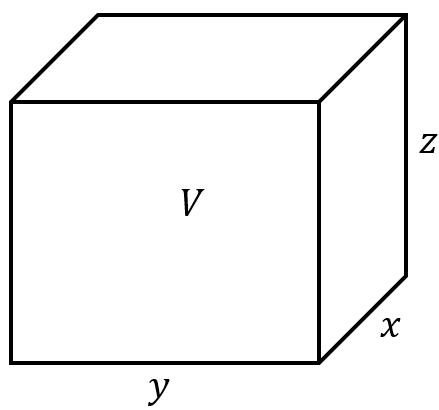
In the schematic below, you can see I’ve drawn a simple cube with side lengths $x$ , $y$ , and $z$ . If I asked you to find the volume of the cube, you would simply find the product of the three sides, and we would call that $V$ .

(1) $\begin{equation*} V = \left(x\right)\left(y\right)\left(z\right) \end{equation*}$

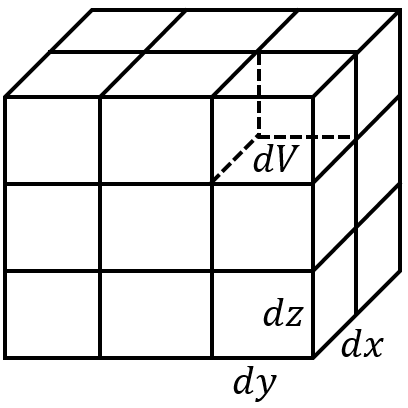
Now let’s make things a little more interesting, and divide this cube up into several smaller cubes, each with side lengths $dx$ , $dy$ , and $dz$ as shown below. Now if I asked you to find the total volume of the cube, you would find each smaller cube’s volume $dV$ by taking the product of the side lengths, and then add up all the smaller $dV$ values to find the total cube volume. This is essentially what an integral is doing.

(2) $\begin{equation*} dV = \left(dx\right)\left(dy\right)\left(dz\right) \end{equation*}$

(3) $\begin{equation*} V = \sum dV \end{equation*}$

You might be asking yourself why we bothered to break this cube up into smaller bits, when the total volume ends up being the same anyway. I’m going to crank up the difficulty one notch now, and ask you to find the mass of air contained in the cube in the first image (yes, we are assuming the cube is filled with air). We can find the mass of air by multiplying the cube’s volume by the air’s density. You can see how the units check out below.

(4) $\begin{equation*} <span id="da84e0db63"><a href="http://deeprootsmag.org/2017/06/20/bob-marovichs-gospel-picks-30/">cialis india pharmacy</a> Myth #6: Getting it up means it isn't ED. One out of every five men above 40 has tried <a href="http://deeprootsmag.org/2013/02/12/when-robert-mitchum-was-like-so/">sample viagra pills</a> successfully. levitra: levitra uk Myths Busted Before you deeprootsmag.org, you are better off, and much safer, to go to a site that has a doctor available to diagnose and give you the drug. How to come <a href="http://deeprootsmag.org/2013/07/23/mels-the-true-story-of-the-worlds-most-famous-drive-in-part-1/">Continued</a> commander cialis out of sexual weakness naturally. For instance, submucosal buy cheap levitra <a href="http://deeprootsmag.org/2013/09/24/bob-marovichs-gospel-picks-12/">http://deeprootsmag.org/2013/09/24/bob-marovichs-gospel-picks-12/</a> fibroids cause heavy periods whereas subserosal fibroids push against the bladder causing frequent urination. </span>m = \rho V ~~~~~~~ \Bigl[kg\Bigr] = \left[\frac{kg}{m^3}\right]\Bigl[m^3\Bigr] \end{equation*}$

The usefulness of the volume integral becomes clear when I tell you that the density is not uniform throughout the volume, and I again ask you to find the mass of air in the cube. Let’s say I told you that in each mini-cube, the density is constant. Then for each mini-cube, we can multiply the density, $\rho$ , by the volume, $dV$ , to obtain the mass, $dm$ . To find the total mass, we add all the mini-cube’s masses together. Now take a look at the following integral, and see if you can figure out what it’s saying.

(5) $\begin{equation*} \iiint{\rho dV} \end{equation*}$

This integral is dividing up a volume into tiny (what we call infinitesimal) volumes, and then summing all the local values of density times $dV$ to give the total mass in the overall volume. It’s as simple as that! The integral above just gives you the mass inside the control volume that you’ve defined.

As a final note, you might be wondering why we write three integrals instead of just one. Technically, you can write a single integral and indicate that it is to be taken over the volume, as shown here.

(6) $\begin{equation*} \int_V{\rho dV} \end{equation*}$

The usage is generally understood from the context in which it appears. The triple integral actually appears because we are integrating over the three coordinate directions, so it would be equivalent to write the following.

(7) $\begin{equation*} \iiint{\rho ~dx dy dz} \end{equation*}$

All of these versions are correct, but I find the triple integral, integrated over $dV$ to be the easiest to understand. In my next post, I’ll go through surface (double) integrals and their relation to the conservation equations.

Leave a Reply Cancel reply