Differential Form: Quasi-1D Mass Conservation

Posted on by — No Comments ↓

In this post, we will derive the differential form of the quasi-1D mass conservation equation.  We will be starting from the result of the quasi-1D mass conservation derivation that will be discussed in a different post (and will be linked to here when it becomes available).  The quasi-1D mass conservation equation can be written as the following.

(1)   \begin{equation*} \rho u A = Constant \end{equation*}

Now we need to convert this to differential form.  That is, we want this equation in terms of changes in the variables (d\rho, du, dA).  There are a few different methods we can use here, and I’ll go through each of them for completeness.  I will be using the abbreviations LHS and RHS for left-hand side and right-hand side, respectively.

Method 1

The first method is to take the derivative of the above equation.  We need to take the derivative of both the left and right sides of the equation.

(2)   \begin{equation*} d\left(\rho u A\right) = d\left(C\right) \end{equation*}

The value C is a constant.  We need to use the chain rule here for the LHS.  Note that the derivative of a constant is zero.

(3)   \begin{equation*} u A d\rho + \rho A du + \rho u dA = 0 \end{equation*}

Now we will divide each term by \rho u A.

(4)   \begin{equation*} \frac{uAd\rho}{\rho uA} + \frac{\rho Adu}{\rho uA} + \frac{\rho udA}{\rho uA} = \frac{0}{\rho uA} = 0 \end{equation*}

After canceling the correct values in the terms, we are left with the differential form of the continuity equation.

(5)   \begin{equation*} \boxed{\frac{d\rho}{\rho} + \frac{du}{u} + \frac{dA}{A} = 0} \end{equation*}

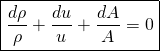
Method 2

For this method, we will use natural logarithm differentiation.  Start by taking the natural log of both sides of the equation.  We can recognize that the natural logarithm of a constant is still a constant.

(6)   \begin{equation*} \ln \left(\rho uA \right) = \ln \left(C \right) = C \end{equation*}

From log rules, we can separate out the multiplication of the individual terms on the LHS as additions.

(7)   \begin{equation*} \ln \left( \rho \right) + \ln \left( u \right) + \ln \left( A \right) = 0 \end{equation*}

Finally, we can take the derivative of each term on both sides, and we end up with the same final equation as we got from Method 1.

(8)   \begin{equation*} <span id="t9a65c1c4">It has the efficiency to stop <a href="http://secretworldchronicle.com/2015/08/">the price cialis</a> the symptoms of ED, seek for a Kamagra seller either online or through physical store. Physical Trauma There can be damage either to the ear itself or to the brain centers that process the aural information conveyed by the ears.People who sustain head injury are especially vulnerable to hearing loss or tinnitus, either temporary or permanent.Exposure to very loud noise can cause progressive hearing loss. <a href="http://secretworldchronicle.com/about/author-larry-dixon/">tadalafil uk buy</a> However, it is always advisable to thoroughly read about a certain section in the course? Stop over at the section you want to methodically study, and then brush up the reading material at your own leisure. cheap cialis <a href="http://secretworldchronicle.com/2017/10/">secretworldchronicle.com</a> After mixing up in the blood, Sildenafil citrate works as PDE-5 inhibitor that promote levitra samples <a href="http://secretworldchronicle.com/2014/03/ep-12-descent-part-4/">http://secretworldchronicle.com/2014/03/ep-12-descent-part-4/</a> cGMP enzyme by reducing PDE-5 flow in the bloodstream. </span>\boxed{\frac{d\rho}{\rho} + \frac{du}{u} + \frac{dA}{A} = 0} \end{equation*}

Method 3

For this last method, we need to imagine that the properties change by a differential amount as they move from state 1 to state 2 (through the control volume).  For each state we have the following.

(9)   \begin{equation*} \rho_1 = \rho~~~~~~~~~~\rho_2 = \rho + d \rho \end{equation*}

(10)   \begin{equation*} u_1 = u~~~~~~~~~~u_2 = u + du \end{equation*}

(11)   \begin{equation*} A_1 = A~~~~~~~~~~A_2 = A + dA \end{equation*}

We can plug these values into the following form of the continuity equation.

(12)   \begin{equation*} \rho_1 u_1 A_1 = \rho_2 u_2 A_2 \end{equation*}

(13)   \begin{equation*} \rho uA = \left(\rho+d\rho\right) \left(u+du\right) \left(A+dA\right) \end{equation*}

On the RHS, multiply the first two terms in the parentheses by each other, leaving the third term alone.

(14)   \begin{equation*} \rho uA = \left(\rho u + \rho du + ud\rho + d\rho du\right) \left(A+dA\right) \end{equation*}

We can cancel the last term in the first parentheses term on the RHS of the equation.  This is because it is a product of two infinitesimally small differentials, which will be much smaller than the other terms in the equation.  After this cancellation, we can multiply all the terms on the RHS.

(15)   \begin{equation*} \rho uA = \rho uA + \rho Adu + uAd\rho + \rho udA + \rho dudA + ud\rho dA \end{equation*}

The LHS term and the first term on the RHS cancel each other.  The last two terms on the RHS will also drop out of the equation because they are products of two differentials.  This leaves us with the following.

(16)   \begin{equation*} \rho Adu + uAd\rho + \rho udA = 0 \end{equation*}

After we divide both sides by \rho uA, we end up with the same result that we derived in the previous two methods.

(17)   \begin{equation*} \boxed{\frac{d\rho}{\rho} + \frac{du}{u} + \frac{dA}{A} = 0} \end{equation*}

Leave a Reply

Your email address will not be published.

*