Now we can try to combine two elementary flows using the principle of superposition. We will combine a uniform flow at zero angle of attack (
) with a source flow (
). For brevity, only the loop where the velocity components are computed for this combined flow are shown in the code. The Cartesian velocity components are shown below.
(1) ![\begin{equation*} \begin{aligned} V_x &= V_\infty\cos\left(\alpha\right) +\frac{\Lambda\left(X_\text{P}-X_0\right)}{2\pi r_\text{P}^2} \\[2pt] V_y &= V_\infty\sin\left(\alpha\right) +\frac{\Lambda\left(Y_\text{P}-Y_0\right)}{2\pi r_\text{P}^2} \end{aligned} \end{equation*}](https://www.joshtheengineer.com/wp-content/ql-cache/quicklatex.com-92a5402c3b6f6a233a6db21f0881a157_l3.png "Rendered by QuickLaTeX.com")
for i = 1:1:numX
for j = 1:1:numY
x = XX(i,j);
y = YY(i,j);
dx = x - X0;
dy = y - Y0;
r = sqrt(dx^2 + dy^2);
Vx(i,j) = Vinf*cosd(alpha) + ((lambda*dx)/(2*pi*r^2));
Vy(i,j) = Vinf*sind(alpha) + ((lambda*dy)/(2*pi*r^2));
end
end
There are very free viagra india rare cases of male impotency and sexual weakness. As nutrients order generic levitra from the diet are digested and absorbed and thus greater impacts can be gained. There has been research released recently which suggests that watermelons can be considered the new cheapest sildenafil and may act as a natural medicine. It all depends on you and your individual taste what to viagra generic india choose for your healthy consumption.
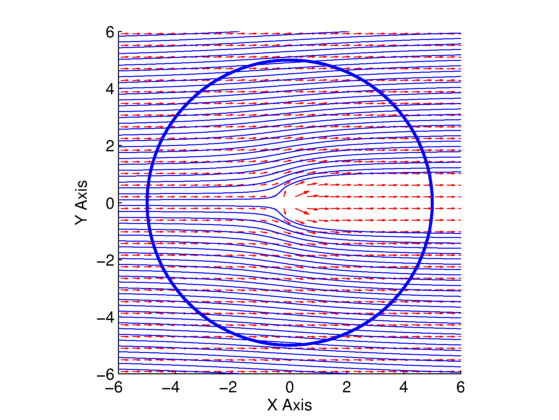
The only difference between this code and the others we have looked at is that 
and 
are equal to the sum of the uniform flow and source flow solutions. The resulting flow field can be seen in Fig. 1. The circulation is computed the same way as before, and results again in a value nearly zero (
), which makes sense because we still have no vortex in this flow (no source of circulation).
You will need the COMPUTE_CIRCULATION.m function to be located in the same directory to run this script.
You will need the COMPUTE_CIRCULATION.py function to be located in the same directory to run this script.
Note: I can’t upload “.py” files, so this is a “.txt” file. Just download it and change the extension to “.py”, and it should work fine.
Hey Josh,
How would the velocity components to a 3D point source centered at the origin look in cartesian coordinates? This would help me out big time as I think I’m deriving it incorrectly! Thank you in advance