Engineering Blog – Page 4 – Josh The Engineer

Volume (Triple) Integrals

Posted on December 22, 2016 by joshtheengineer11@gmail.com — No Comments ↓

In this article I’ll be going through what I think is an intuitive explanation of a volume (or triple) integral in relation to the conservation equations. I’m laying out the volume integral before I go through the less-intuitive surface integral in my next post. As a quick note, I usually write the volume as a $V$ with a strike-through, but I can’t do this using the WordPress Latex interpreter, so whenever you see a normal capital $V$ , don’t confuse it with the velocity vector, $\vec{V}$ .

In the schematic below, you can see I’ve drawn a simple cube with side lengths $x$ , $y$ , and $z$ . If I asked you to find the volume of the cube, you would simply find the product of the three sides, and we would call that $V$ .

(1) $\begin{equation*} V = \left(x\right)\left(y\right)\left(z\right) \end{equation*}$

Continue reading Volume (Triple) Integrals→

Solving the Area-Mach Number Relation

Posted on November 16, 2016 by joshtheengineer11@gmail.com — 6 Comments ↓

Introduction

The area-Mach number relation (AMR from now on), is important when analyzing nozzle flows. In this post, I’m not going to go through the derivation of the equation because I derive it in this video. I will be taking the final equation and showing you a few different methods of solution, along with some MATLAB code that you can use in your own programs. Below is the equation we will be looking at.

(1) $\begin{equation*} \left( \frac{A}{A^*} \right) ^2 = \frac{1}{M^2} \left[ \frac{2}{\gamma + 1} \left(1+\frac{\gamma -1}{2} M^2 \right) \right]^{\frac{\gamma + 1}{\gamma -1}} \end{equation*}$

The term $\frac{A}{A^*}$ is the area ratio, $M$ is the Mach number, and $\gamma$ is the specific heat ratio. There are two ways of looking at this equation. The first is that the area ratio is a function of Mach number, and the second is that the Mach number is a function of the area ratio. It all depends on what you have and what you want to calculate.

Continue reading Solving the Area-Mach Number Relation→

Why Euler’s Formula Works

Posted on September 26, 2016 by joshtheengineer11@gmail.com — No Comments ↓

In many parts of engineering, you’ll run across something called Euler’s formula, which looks something like this.

(1) $\begin{equation*} e^{i\theta} = \cos(\theta) + i\sin(\theta) \end{equation*}$

It’s something you can look at, memorize, and then use in the future. But sometimes it’s nice to know that mathematically, the left side and the right side are in fact equivalent, even if it’s not obvious. While reading Hecht’s Optics book, I came across a footnote that quickly shows that the two sides are equal. Here is the gist of that footnote.

Continue reading Why Euler’s Formula Works→

Example: Harmonic Function Satisfying the Wave Equation

Posted on September 26, 2016 by joshtheengineer11@gmail.com — No Comments ↓

In this post I’m going to work through the math showing that a simple harmonic wave profile/function satisfies the one-dimensional wave equation. The simple harmonic function is given in the following equation. The variable $v$ is the wave speed in the $x$ direction, while $\psi$ is the shape of the profile of the wave.

(1) $\begin{equation*} \psi (x,t) = A\sin[k (x-vt)] = A\sin(kx-kvt) \end{equation*}$

The 1D wave equation that we wish to satisfy is given below.

(2) $\begin{equation*} \frac{\partial ^2 \psi}{\partial x^2} = \frac{1}{v^2} \frac{\partial ^2 \psi}{\partial t^2} \end{equation*}$

Continue reading Example: Harmonic Function Satisfying the Wave Equation→

TI-83 Calculator Program: Prandtl-Meyer Expansion Wave

Posted on September 11, 2016 by joshtheengineer11@gmail.com — 2 Comments ↓

Introduction & Motivation

If you’ve ever taken a gas dynamics (compressible flow) course, you’ve probably spent hours flipping through the tables at the back of the book to find the correct Prandtl-Meyer (PM) angle for your Mach number, or vice versa. This involves first finding the table (A.5 in my Modern Compressible Flow book by John Anderson), then finding the bounding Mach numbers or angles, and finally interpolating to find the correct value you need. Then you’ll likely need to do this many more times for a single problem. You also won’t be able to use the tables when the specific heat ratio isn’t equal to 1.4.

I decided to write a program for my TI-83 Plus graphing calculator, and I’ll show you how to program it. First, I’ll post the entire program, so if you already know where to find all the commands and such, you can just enter in what you see below. For those who need a little guidance on where to find the commands, I’ll go through them in detail after the entire program code. I’ll also go through how to use the program, and we will check it against the online VT calculator.

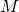The first equation shown below is what we will use to solve for the PM angle $\nu$ . The second equation is used to solve for the Mach number $M$ . The only difference between the two is that the first equation can be solved directly, while in the second equation we are searching for the value of $M$ that makes the function zero.

$\nu(M) = \sqrt{\frac{\gamma +1}{\gamma - 1}} \ tan^{-1} \sqrt{\frac{\gamma - 1}{\gamma + 1}(M^2-1)} - tan^{-1} \sqrt{M^2-1}$

$\nu - \sqrt{\frac{\gamma +1}{\gamma - 1}} \ tan^{-1} \sqrt{\frac{\gamma - 1}{\gamma + 1}(M^2-1)} - tan^{-1} \sqrt{M^2-1} = 0$

Continue reading TI-83 Calculator Program: Prandtl-Meyer Expansion Wave→